Validation of the model
The three solvers used by dBSea are based on codes widely used and tested within the underwater acoustics industry. They have been extensively tested against measured data and analytical solutions. The solver input is written so as to provide accurate results covering a wide range of scenarios which are likely to be of interest to practising acoustics professionals.
Results for a range of benchmark problem comparisons are presented here. Each is shown in cross-section, with the sound source at the left edge of the image.
Reference codes used are from the AcTUP toolbox and OceanAcoustics Library: RAM for the parabolic equation solver, Kraken for the normal modes solver and Bellhop for the raytracer.
The following wedge profile is a low frequency, shallow water problem with a sloping bottom, it follows Jensen & Ferla (1989) [ASA Benchmark paper], and is defined as scetched below.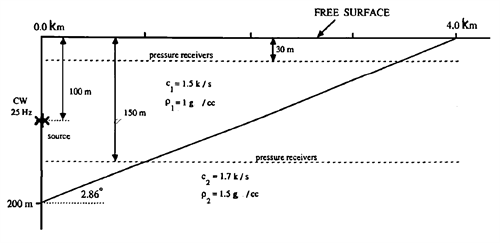
dBSeaPE, dBSeaModes, RAM and Kraken solvers: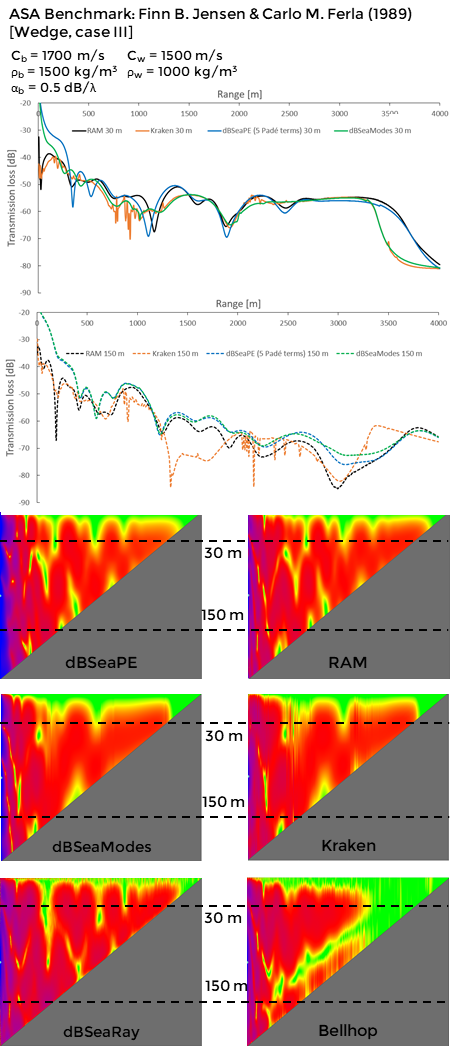
(Please note that due to non-native implementation of the Kraken, solver some irregularities are present, especially around 900 m and 2200 m)
Download UWA file of this scenario (can be viewed with dBSea BASIC)
Further Benchmark Problems:
Sturm (2008), a shallow water wedge problem defined as:
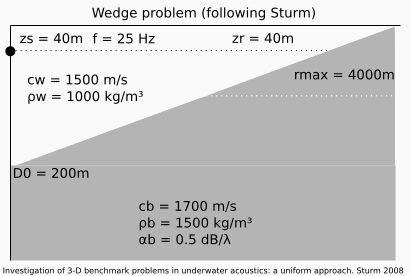
Reference codes used are from the AcTUP toolbox: RAM for the parabolic equation solver, Kraken for the normal modes solver and Bellhop for the raytracer. Received levels are plotted along a single depth.
Summary of dSBea solvers and opensource solvers:
(Note that 25 Hz is very low for the ray tracers [dBSeaRay & Bellhop], but results are included for the sake of completeness).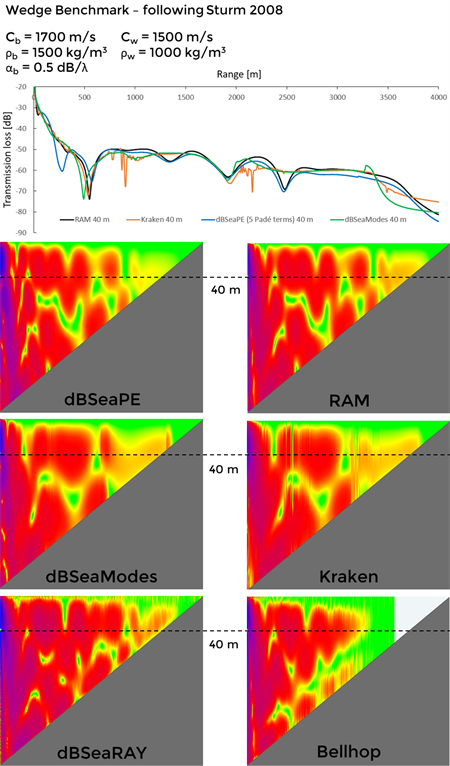
dBSeaRay does not currently penetrate the sediment and so the transmission loss at ranges over ~3200 m become infinite (no levels present). Compare predictions of the shallow water area from dBSeaRay and Bellhop with those from the low-frequency solvers.
Seamount Benchmark Problem:
This example follows "Test Case II" from "PE workshop 1993".
An upslope followed by a downslope tests enegy conservation in a range-dependent environment.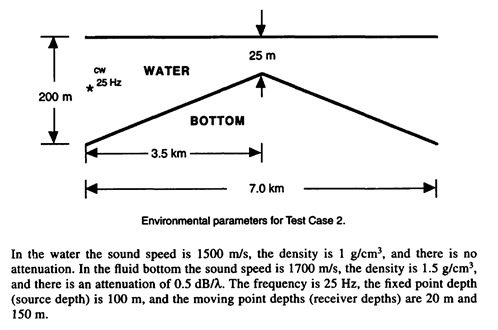
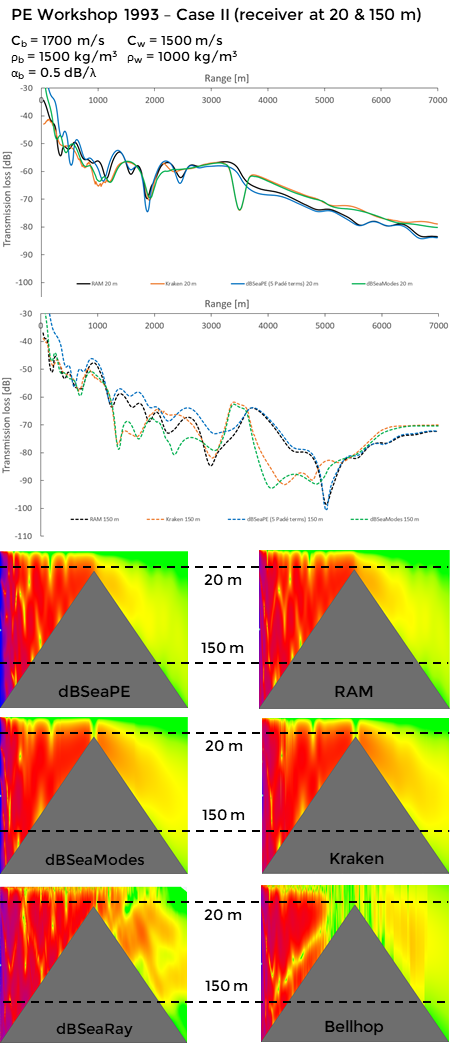
Please note that neither of the ray tracers (dBSeaRay & Bellhop) are suitable for this frequency and don't penetrate the sediment, and their results are only included for completeness.
Flat, level bottom, Pekeris problem:
A horizontal waveguide with depth of 200m, a 25 Hz source at 100 m depth. Received levels at 100 m.

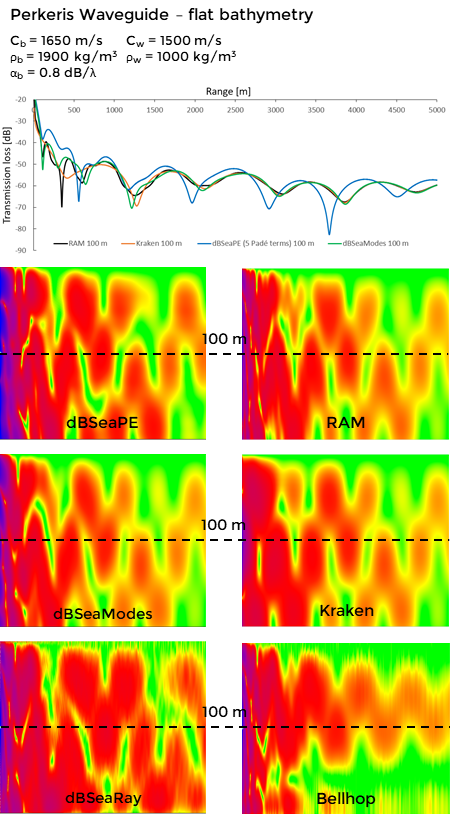
Notice that dBSeaRay produces results very close to the other solvers even in a low frequency problem (25 Hz) such as this.
Further examples with varying bathymetry
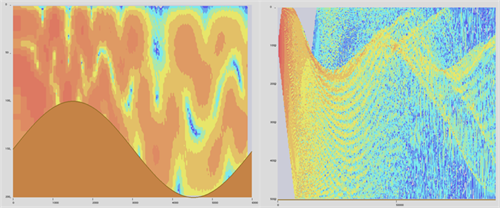
The sinusoidal profile is a low frequency, shallow water problem with a sinusoidal bottom. This problem requires solvers that are able to account for energy which enters the ocean sediment and then is later returned to the water column. The Munk profile is a low frequency, long range, deep water problem with a sound speed profile given by a formula with a minimum leading to a sound channel at around 1000 - 2000m depth.